The arithmetic sequence, 1487, 4817, 8147, in which each of the terms increases by 3330, is unusual in two ways: (i) each of the three terms are prime, and, (ii) each of the 4-digit numbers are permutations of one another.
There are no arithmetic sequences made up of three 1-, 2-, or 3-digit primes, exhibiting this property, but there is one other 4-digit increasing sequence.
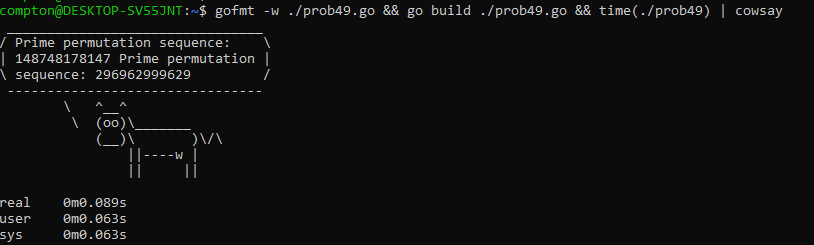
What 12-digit number do you form by concatenating the three terms in this sequence?
Here is my solution in Golang.
////////////////////////////////////////////////////////////////////////////////
package main
////////////////////////////////////////////////////////////////////////////////
import (
"fmt"
"sort"
)
////////////////////////////////////////////////////////////////////////////////
func main() {
sieve := sieveOfErastothenes(10000)
for i := 1000; i <= 9999; i++ {
if sieve[i] == false {
for j := 1; i+(2*j) <= 9999; j++ {
if !(sieve[i+j]) && !(sieve[i+(2*j)]) {
if permCheck(i, i+j, i+(2*j)){
fmt.Printf("Prime permutation sequence: %d%d%d\n", i, i+j, i+(2*j))
}
}
}
}
}
}
////////////////////////////////////////////////////////////////////////////////
func sieveOfErastothenes(maxVal int) []bool {
sieve := make([]bool, maxVal)
for i := 2; i < 10000; i++ {
if(sieve[i] == false){
for j := i * 2; j < (10000 - i); j += i {
sieve[j] = true
}
}
}
return sieve
}
////////////////////////////////////////////////////////////////////////////////
func digSepSort(a int) (digBuff []int) {
for a != 0 {
modBuff := (a % 10)
a /= 10
digBuff = append(digBuff, modBuff)
}
sort.Ints(digBuff)
return digBuff
}
////////////////////////////////////////////////////////////////////////////////
func permCheck(a int, b int, c int) bool {
digBuffA := digSepSort(a)
digBuffB := digSepSort(b)
digBuffC := digSepSort(c)
for i := 0; i < 4; i++ {
if digBuffA[i] != digBuffB[i] {
return false
}
if digBuffB[i] != digBuffC[i] {
return false
}
}
return true
}
////////////////////////////////////////////////////////////////////////////////
