Problem 44: Pentagon Numbers

Pentagonal numbers are generated by the formula, P_n=n(3n−1)/2. The first ten pentagonal numbers are:

1, 5, 12, 22, 35, 51, 70, 92, 117, 145, …

It can be seen that P₄ + P₇ = 22 + 70 = 92 = P₈. However, their difference, 70 − 22 = 48, is not pentagonal.

Find the pair of pentagonal numbers, P_j and P_k, for which their sum and difference are pentagonal and D = |P_k − P_j| is minimised; what is the value of D?

Here is my solution in Golang

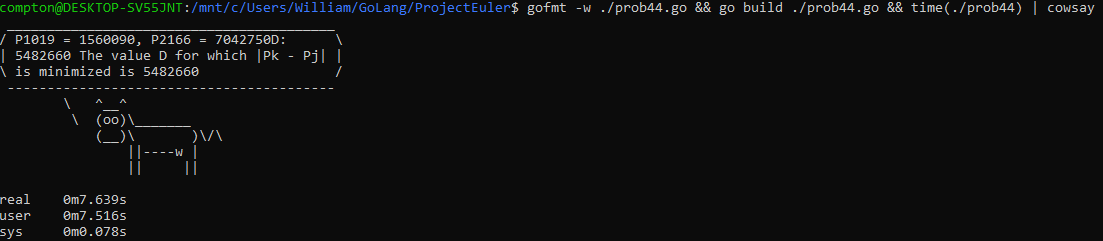
package main

import (
	"fmt"
)

func main() {
	pentagonalList := pentagonalGenerate(2500)
	d := pentagonalList[len(pentagonalList)-1] // high number to seed d
	for i := 0; i < len(pentagonalList)-1; i++ {
		for j := i + 1; j < len(pentagonalList); j++ {
			if (pentagonalList[j] - pentagonalList[i]) < d {	
				if pentSumDiffCheck(pentagonalList[i], pentagonalList[j], pentagonalList) {
					d = pentagonalList[j] - pentagonalList[i]
					fmt.Printf("P%d = %d, P%d = %d", i, pentagonalList[i], j, pentagonalList[j])
					fmt.Println("D: ", d)
				}
			}
		}
	}
	fmt.Println("The value D for which |Pk - Pj| is minimized is ", d)
}

func pentagonalGenerate(pentCount int) []int {
	pentagonalList := make([]int, 0)
	for i := 1; i < pentCount; i++ {
		pentagonalList = append(pentagonalList, (i * ((3 * i) - 1) / 2))
	}
	return pentagonalList
}

func pentSumDiffCheck(i int, j int, pentagonalList []int) bool {
	sum := i + j
	diff := j - i
	var sumFlag, diffFlag bool
	for k := 0; k < len(pentagonalList); k++ {
		if (sumFlag == true) && (diffFlag == true) {
			return true
		}
		if sum == pentagonalList[k] {
			sumFlag = true
		}
		if diff == pentagonalList[k] {
			diffFlag = true
		}
	}
	return false
}