Triangle, pentagonal, and hexagonal numbers are generated by the following formulae:
| Triangle | Tn=n(n+1)/2 | 1, 3, 6, 10, 15, … |
| Pentagonal | Pn=n(3n−1)/2 | 1, 5, 12, 22, 35, … |
| Hexagonal | Hn=n(2n−1) | 1, 6, 15, 28, 45, … |
It can be verified that T285 = P165 = H143 = 40755.
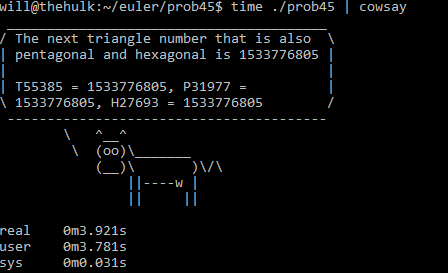
Find the next triangle number that is also pentagonal and hexagonal.
Here is my solution in Golang!
package main
import (
"fmt"
"sync"
)
func main() {
var triList, pentList, hexList []uint64
nMax := 5000
nSeed := nMax
// Start at n = 285, since that is the lower bounds for the question
nStart := 286
listGen(nMax, 0, &triList, &pentList, &hexList)
for !triCheck(nStart, nMax, triList, pentList, hexList) {
// Start at what was previously the max
nStart = nMax
// Increase the max value to calculate for n
nMax += 1000
listGen(nMax, nSeed, &triList, &pentList, &hexList)
// Preserve nMax for next loop to know where to start calculating to append to lists
nSeed = nMax
}
}
func triGen(nMax int, nSeed int, triList *[]uint64) {
triCalc := func(i uint64) uint64 {
return ((i * (i + 1)) / 2)
}
for i := uint64(nSeed); i < uint64(nMax); i++ {
*triList = append(*triList, triCalc(i) )
}
return
}
func pentGen(nMax int, nSeed int, pentList *[]uint64) {
pentCalc := func(i uint64) uint64 {
return ((i * ((3 * i) - 1)) / 2)
}
for i := uint64(nSeed); i < uint64(nMax); i++ {
*pentList = append(*pentList, pentCalc(i))
}
return
}
func hexGen(nMax int, nSeed int, hexList *[]uint64) {
hexCalc := func(i uint64) uint64 {
return (i * ((2 * i) - 1))
}
for i := uint64(nSeed); i < uint64(nMax); i++ {
*hexList = append(*hexList, hexCalc(i))
}
return
}
func listGen(nMax int, nSeed int, triList *[]uint64, pentList *[]uint64, hexList *[]uint64) {
var wg sync.WaitGroup
wg.Add(3)
// Spawn routines to calculate next sets of numbers
go func(){
defer wg.Done()
triGen(nMax, nSeed, triList)
}()
go func(){
defer wg.Done()
pentGen(nMax, nSeed, pentList)
}()
go func(){
defer wg.Done()
hexGen(nMax, nSeed, hexList)
}()
wg.Wait()
}
func triCheck(nStart int, nMax int, triList []uint64, pentList []uint64, hexList []uint64) bool {
for i := nStart; i < nMax; i++ {
for j := 0; j < nMax; j++ {
// If the pentagonal number is greater than the triangle, I know to increment the triangle!
if pentList[j] > triList[i] {
break
}
// Else if they are equal, I know to start checking for a hexList match
if pentList[j] == triList[i] {
for k := 0; k < nMax; k++ {
// If the hexList value is now greater than the pentList value, I know to increment pentList, which will in turn increment triList
if hexList[k] > pentList[j] {
break
} else {
if hexList[k] == pentList[j] && pentList[j] == triList[i] {
fmt.Printf("The next triangle number that is also pentagonal and hexagonal is %v\n ", triList[i])
fmt.Printf("T%v = %v, P%v = %v, H%v = %v", i, triList[i], j, pentList[j], k, hexList[k])
return true
}
}
}
}
}
}
return false
}
