It can be seen that the number, 125874, and its double, 251748, contain exactly the same digits, but in a different order.
Find the smallest positive integer, x, such that 2x, 3x, 4x, 5x, and 6x, contain the same digits.
Here is my solution in Golang.
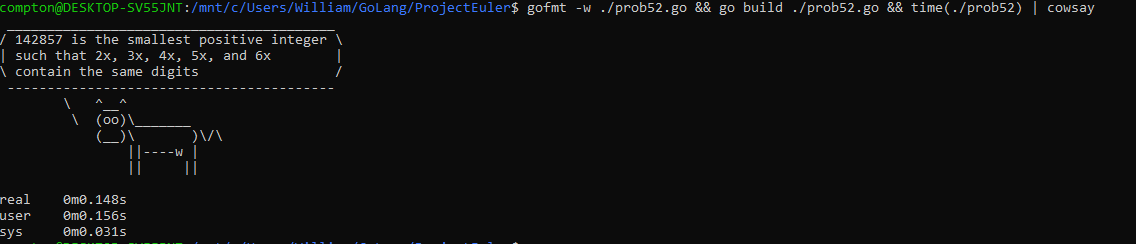
package main
import (
"fmt"
"sort"
)
func main() {
for i := 1; ; i++ {
if permCheck(i) {
fmt.Printf("%d is the smallest positive integer such that 2x, 3x, 4x, 5x, and 6x contain the same digits", i)
break
}
}
return
}
func digSepAndSort(foo int) []int {
digBuff := make([]int, 0)
for foo != 0 {
modBuff := foo % 10
digBuff = append(digBuff, modBuff)
foo /= 10
}
sort.Ints(digBuff)
return digBuff
}
func permCheck(foo int) bool {
a := digSepAndSort(foo)
if sliceEquality(a, digSepAndSort(2*foo)) {
if sliceEquality(a, digSepAndSort(3*foo)) {
if sliceEquality(a, digSepAndSort(4*foo)) {
if sliceEquality(a, digSepAndSort(5*foo)) {
if sliceEquality(a, digSepAndSort(6*foo)) {
return true
}
}
}
}
}
return false
}
func sliceEquality(a []int, b []int) bool {
for i := 0; i < len(a); i++ {
if a[i] != b[i] {
return false
}
}
return true
}
