Problem 46: Goldbach’s other conjecture

It was proposed by Christian Goldbach that every odd composite number can be written as the sum of a prime and twice a square.

9 = 7 + 2×1²
15 = 7 + 2×2²
21 = 3 + 2×3²
25 = 7 + 2×3²
27 = 19 + 2×2²
33 = 31 + 2×1²

It turns out that the conjecture was false.

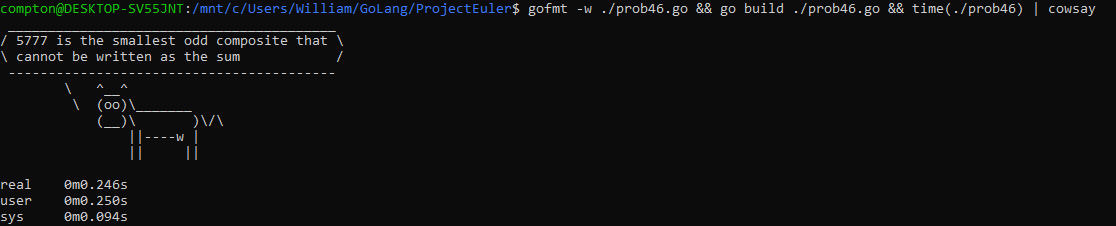
What is the smallest odd composite that cannot be written as the sum of a prime and twice a square?

////////////////////////////////////////////////////////////////////////////////
package main
////////////////////////////////////////////////////////////////////////////////
import (
	"fmt"
	"math"
)
////////////////////////////////////////////////////////////////////////////////
func main() {
	sieve := sieveOfErastothenes(100000) // Arbitrary prime max, I'm guessing!
	for i := 9; i < len(sieve); i += 2 {
		if sieve[i] == true {
			if goldbachCheck(i, sieve) == false {
				fmt.Printf("%d is the smallest odd composite that cannot be written as the sum", i)
				break
			}
		}
	}
	return
}
////////////////////////////////////////////////////////////////////////////////
func sieveOfErastothenes(maxVal int) []bool {
	sieve := make([]bool, maxVal)
	for i := 2; i < 10000; i++ {
		for j := i * 2; j < (10000 - i); j += i {
			sieve[j] = true
		}
	}
	return sieve
}
////////////////////////////////////////////////////////////////////////////////
func goldbachCheck(composite int, primeList []bool) bool {
	for i := 2; i < 10000; i++ {
		if primeList[i] == false {
			if i > composite {
				break
			} else {
				for j := 1; ; j++ {
					k := (i + 2*(int(math.Pow(float64(j), float64(2)))))
					if k > composite {
						break
					}
					if k == composite {
						return true
					}
				}
			}
		}
	}
	return false
}
////////////////////////////////////////////////////////////////////////////////