Solving a second order linear homogenous recurrence relation with consistent coefficients

#include <iostream>
#include <vector>
#include <math.h>

// Solves for quadratic formula
std::vector quadraticCalc(double a, double b, double c);

int main(void)
{
	double A = 0, B = 0, Cone, Ctwo;
	std::vector<double> terms, quadBuff;

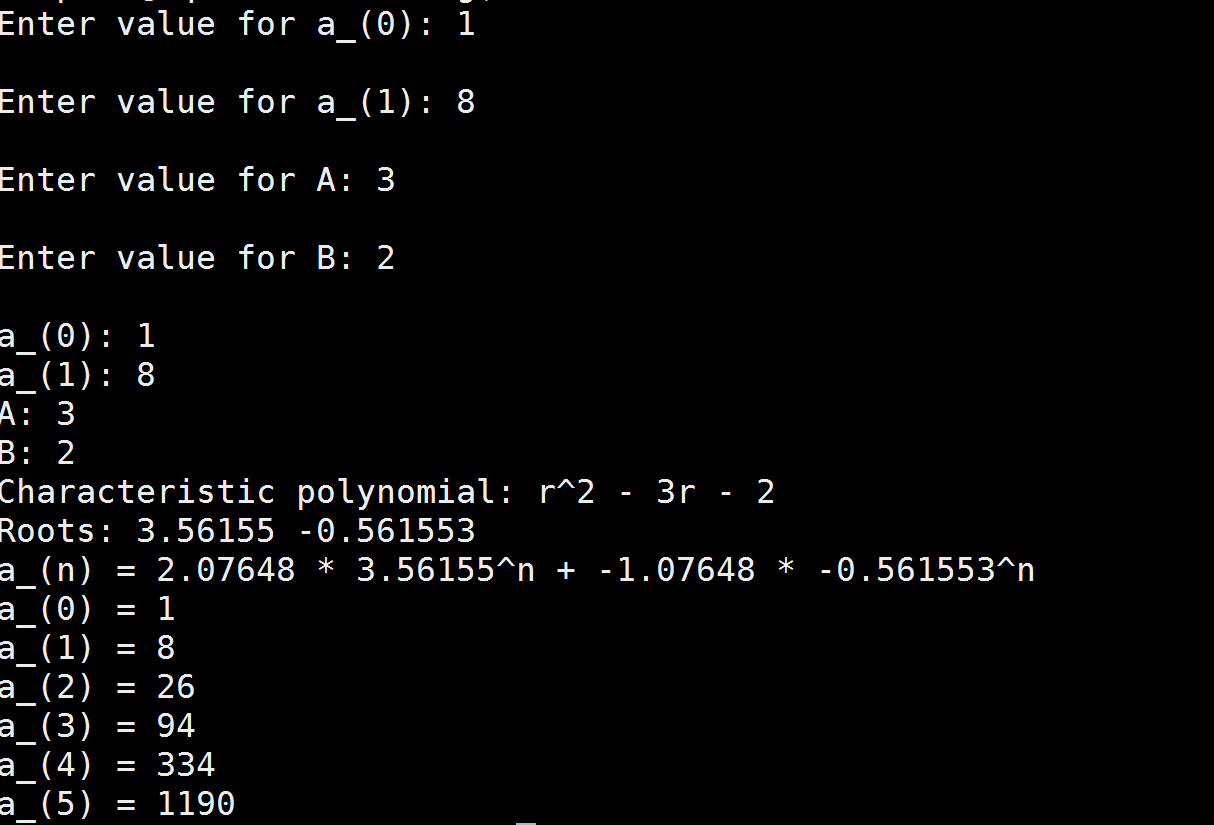
	std::cout << "Enter value for a_(0): "; std::cin >> A;
	terms.push_back(A);
	std::cout << std::endl;

	std::cout << "Enter value for a_(1): "; std::cin >> A;
	terms.push_back(A);
	std::cout << std::endl;

	std::cout << "Enter value for A: "; std::cin >> A;
	std::cout << std::endl;

	std::cout << "Enter value for B: "; std::cin >> B;
	std::cout << std::endl;

	std::cout << "a_(0): " << terms[0] << "\n" << "a_(1): " << terms[1] << "\n" << "A: " << A << "\n" << "B: " << B << "\n";

	std::cout <<  "Characteristic polynomial: " << "r^2 - " << A << "r - " << B << "\n";
	// Calculate characteristic polynomial using quadratic formula
	quadBuff = quadraticCalc(1, A, -B);
	// If the roots are discrete
	if(quadBuff[0] != quadBuff[1])
	{
		std::cout << "Roots: ";
		// Output roots
		for(auto rootIt : quadBuff)
		{
			std::cout << rootIt << " ";
		}
		// Set C_(2) equal to (a_(1) - r_(1)) / (r_(2) - r_(1))
		Ctwo = (terms[1] - quadBuff[0]) / (quadBuff[1] - quadBuff[0]);
		// Set C_(1) equal to a_(0) - C_(2), as a_(0) is equal to C_(1) + C_(2)
		Cone = terms[0] - Ctwo;
		// Output "formula", or a_(n) = C_(1)*(r_(1))^n + C_(2) * r_(2)^n
		std::cout << "\na_(n) = " << Cone << " * " << quadBuff[0] << "^n + " << Ctwo << " * " << quadBuff[1] << "^n\n";

		for(int i = 2; i < 6; i++)
		{
			terms.push_back((Cone * pow(quadBuff[0], i)) + (Ctwo * pow(quadBuff[1], i)));
		}
	}
	// It is a repeated root
	else
	{
		std::cout << "Root: " << quadBuff[0] << std::endl;
		std::cout << "a_(n) = C_(1)" << quadBuff[0] << "^n + C_(2)n" << quadBuff[0] << "^n\n";
		// C_(1) = a_(0)
		Cone = terms[0];
		std::cout << "C_(1) = " << Cone;
		// a_(1) = C_(1)*r + C_(2)*r, where r is the repeated characteristic polynomial root
		Ctwo = terms[1] - (Cone * quadBuff[0]);
		Ctwo /= quadBuff[0];
		std::cout << "C_(2) = " << Ctwo;
		for(int i = 2; i < 6; i++)
		{
			// Solve for C_(1)r^n + C_(2)nr^n
			terms.push_back((Cone * pow(quadBuff[0], i)) + (Ctwo * i * pow(quadBuff[0], i)));
		}
	}
	// Output the terms
	for(int i = 0; i < 6; i++)
	{
		std::cout << "a_(" << i << ") = " << terms[i] << std::endl;
	}

	return 0;
}


std::vector quadraticCalc(double a, double b, double c)
{
	std::vector<double> roots;
	double rootBuff;
	// If there is a complex root
	if((pow(b, 2) - (4*a*c)) < 0)
	{
		std::cout << "Complex root found\n Exiting now";
		exit(-1);
	}
	// Push back the two roots
	roots.push_back(-((-b) - sqrt( (b*b) - (4*a*c))) / (2*a));

	roots.push_back(-((-b) + sqrt( (b*b) - (4*a*c))) / (2*a));

	return roots;
}