If we take 47, reverse and add, 47 + 74 = 121, which is palindromic.
Not all numbers produce palindromes so quickly. For example,
349 + 943 = 1292,
1292 + 2921 = 4213
4213 + 3124 = 7337
That is, 349 took three iterations to arrive at a palindrome.
Although no one has proved it yet, it is thought that some numbers, like 196, never produce a palindrome. A number that never forms a palindrome through the reverse and add process is called a Lychrel number. Due to the theoretical nature of these numbers, and for the purpose of this problem, we shall assume that a number is Lychrel until proven otherwise. In addition you are given that for every number below ten-thousand, it will either (i) become a palindrome in less than fifty iterations, or, (ii) no one, with all the computing power that exists, has managed so far to map it to a palindrome. In fact, 10677 is the first number to be shown to require over fifty iterations before producing a palindrome: 4668731596684224866951378664 (53 iterations, 28-digits).
Surprisingly, there are palindromic numbers that are themselves Lychrel numbers; the first example is 4994.
How many Lychrel numbers are there below ten-thousand?
NOTE: Wording was modified slightly on 24 April 2007 to emphasise the theoretical nature of Lychrel numbers.
This is my solution in Golang… Was getting some weird errors until I realized the sign bit was the cause, hence the casting.
package main
import (
"fmt"
"math"
)
func main() {
lychrelCount := 0
for i := 10; i < 10000; i++ {
if lychrelCheck(uint64(i)) {
lychrelCount++
}
}
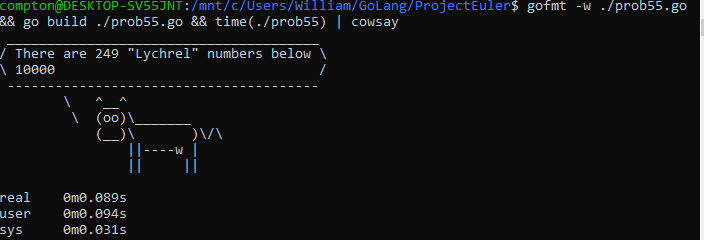
fmt.Printf("There are %d \"Lychrel\" numbers below 10000", lychrelCount)
}
func reverseInt(passedNumb uint64) uint64 {
digitHolder := make([]int, 0)
var reversed uint64
// separate out digits
for passedNumb != 0 {
buff := int((passedNumb % 10))
digitHolder = append(digitHolder, buff)
passedNumb /= 10
}
// multiply by 10^n to place numbers in reverse positions
for i := 0; i < len(digitHolder); i++ {
reversed += uint64(digitHolder[i]) * uint64(math.Pow(10, float64((len(digitHolder)-1)-i)))
}
return reversed
}
func lychrelCheck(lychrelSeed uint64) bool {
cycle := 0
for cycle < 50 {
lychrelSeed = (reverseInt(lychrelSeed) + lychrelSeed)
cycle++
if lychrelSeed == reverseInt(lychrelSeed) {
return false
}
}
return true
}