We shall say that an n-digit number is pandigital if it makes use of all the digits 1 to n exactly once. For example, 2143 is a 4-digit pandigital and is also prime.
What is the largest n-digit pandigital prime that exists?
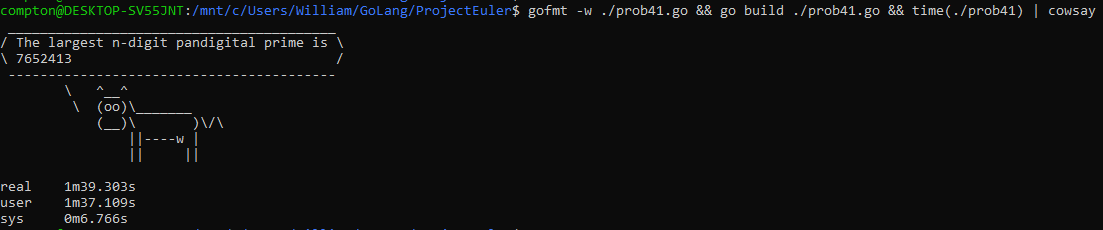
Here is my solution in Golang.
package main
////////////////////////////////////////////////////////////////////////////////
import (
"fmt"
"sort"
)
////////////////////////////////////////////////////////////////////////////////
func main() {
primeList := sieveOfErastothenes(999999999)
primeBuff := 0
for i := 0; i < len(primeList); i++ {
if pandigitalCheck(primeList[i]) {
if primeList[i] > primeBuff {
primeBuff = primeList[i]
}
}
}
fmt.Printf("The largest n-digit pandigital prime is %d", primeBuff)
return
}
////////////////////////////////////////////////////////////////////////////////
func sieveOfErastothenes(maxVal int) []int {
sieve := make([]bool, maxVal)
primeList := make([]int, 0)
for i := 3; i < maxVal; i += 2 {
if sieve[i] == false {
primeList = append(primeList, i)
}
for j := i * 2; j < maxVal; j += i {
sieve[j] = true
}
}
return primeList
}
////////////////////////////////////////////////////////////////////////////////
func pandigitalCheck(i int) bool {
digitBuff := make([]int, 0)
for i != 0 {
j := (i % 10)
i /= 10
digitBuff = append(digitBuff, j)
}
sort.Ints(digitBuff)
for i = 0; i < len(digitBuff); i++ {
if digitBuff[i] != (i + 1) {
return false
}
}
return true
}
////////////////////////////////////////////////////////////////////////////////
